|
|
Computational Design & Manufacturing Lab University of Wisconsin-Madison |
|
||||
|
|
||||||
|
|
Research
Interests
Isogeometric analysis on triangulationsAcknowledgment: This research is supported
in part by NSF grant #1435072 and ARO grant W911NF-17-1-0020.
We have developed a method for isogeometric analysis on the triangulation of a domain bounded by NURBS curves (or surfaces). In this method, both the geometry and the physical field are represented by bivariate (or trivariate) splines in Bernstein–Bézier form over the triangulation. We have developed a set of procedures to construct a parametric domain and its triangulation from a given physical domain, construct Cr-smooth basis functions over the domain, and establish a rational Triangular Bézier Spline (rTBS) based geometric mapping that Cr-smoothly maps the parametric domain to the physical domain and exactly recovers the NURBS boundaries at the domain boundary. As a result, this approach can achieve automated meshing of objects with complex topologies and allow highly localized refinement.
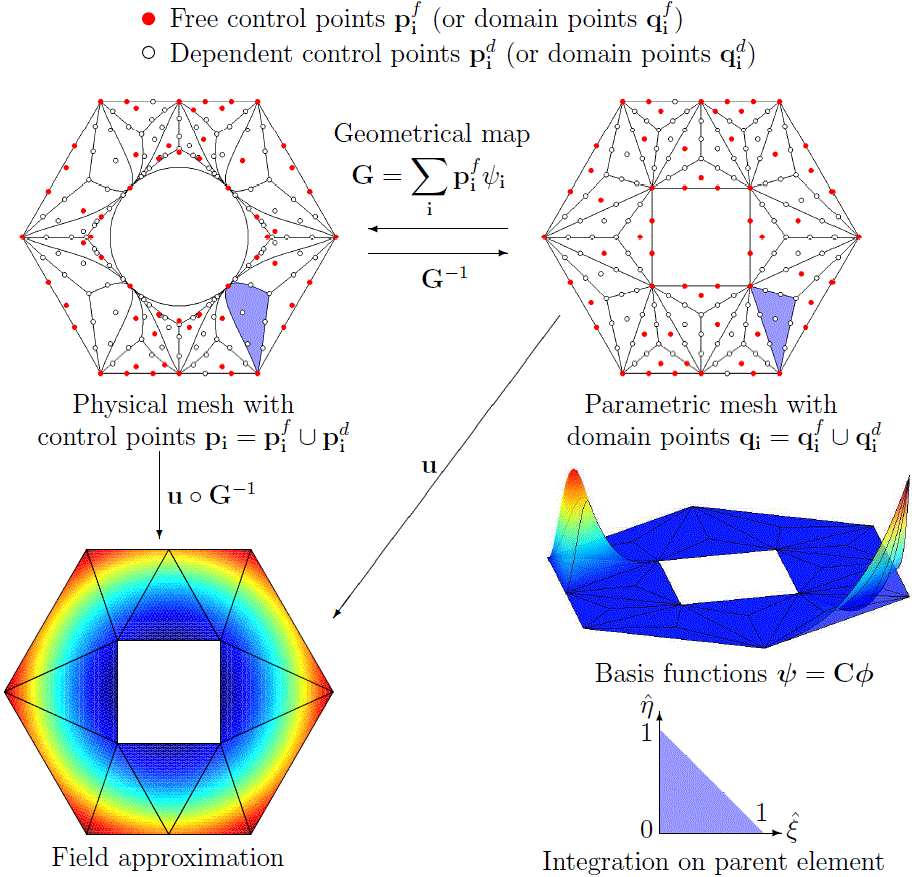
Figure 1Flowchart of isogeometric analysis on triangulations Figure 1 gives a schematic illustration of the flowchart of isogeometric analysis on triangulations. Recently, we have developed a smooth-refine-smooth procedure to achieve optimal convergence with such Cr rTBS basis. We show that the optimal rate of convergence can be achieved provided that the Cr geometric map remains unchanged during the refinement process. This condition can be satisfied by constructing a pre-refinement geometric map that is sufficiently smooth. Numerical experiments verify that optimal rates of convergence are achieved for Poisson and linear elasticity problems. Our approach can automatically convert 3D CAD models into watertight Bezier Tetrahedra. NURBS surfaces without trimmed boundaries are converted to Bezier triangles exactly. Trimmed NURBS surfaces are converted to Bezier triangles with controlled approximation error. Relevant publications
o
Ruochun Zhang
and Xiaoping Qian, ``
Triangulation-based isogeometric analysis of the Cahn-Hilliard phase-field model
,'' Computer Methods in Applied Mechanics and Engineering, Vol. 357,
112569, 2019. [pdf]
o
Mehrdad Zareh
and Xiaoping Qian, ``
Kirchhoff-Love Shell Formulation based on triangular isogeometric analysis
,'' Computer Methods in Applied Mechanics and Engineering, Vol. 347,
853 - 873, 2019. [pdf]
o
Songtao Xia
and Xiaoping Qian, ``
Generating high-quality high-order parameterization for isogeometric analysis on triangulations
,'' Computer Methods in Applied Mechanics and Engineering, Vol. 338,
1-26, 2018. [pdf]
o
Cunfu Wang
Songtao Xia, Xilu Wang and Xiaoping Qian, ``
Isogeometric Shape Optimization on Triangulations
,'' Computer Methods in Applied Mechanics and Engineering, Vol. 338,
1-26, 2018. [pdf]
o
Songtao Xia
and Xiaoping Qian, ``
Isogeometric analysis with Bézier tetrahedra
,'' Computer Methods in Applied Mechanics and Engineering, Vol. 316,
782-816, 2017. [pdf]
o
Songtao Xia, Xilu
Wang and Xiaoping Qian, ``Continuity and convergence in rational triangular Bézier spline based isogeometric
analysis,'' Computer Methods in Applied Mechanics and Engineering, Vol. 297,
292-324, 2015. [pdf]
o
Jaxon,
N. and Qian, X., ``Isogeometric analysis on
triangulations,'' Computer-Aided Design, Special Issue on GD/SPM 2013:
SIAM/ACM Joint Conference on Geometric and Physical Modeling, Vol. 46, pp.
45- 57, 2014. [pdf]
o
Wang,
X. and Qian, X., ``An optimization approach for constructing trivariate B-spline solids,'' Computer-Aided Design,
Special Issue on GD/SPM 2013: SIAM/ACM Joint Conference on Geometric and
Physical Modeling, Vol. 46, pp. 179 - 191, 2014. [pdf]
o
Li, K.
and Qian, X., "Isogeometric analysis and shape
optimization via boundary integral", Proceedings of SIAM/ACM Joint
Conference on Geometric and Physical Modeling (GD/SPM11) (Best Paper Award),
Computer-Aided Design, Vol. 43, No. 11, pp. 1427 - 1437, 2011. [pdf]
o
Qian,
X. and Sigmund, O, "Isogeometric shape
optimization of photonic crystals via Coons patches," Computer Methods
in Applied Mechanics and Engineering, Vol. 200, No. 25 - 28, pp. 2237 - 2255,
2011. [pdf]
o
Qian,
X., "Full Analytical Sensitivities in NURBS based Isogeometric
Shape Optimization," Computer Methods in Applied Mechanics and
Engineering, Vol. 199, No. 29 -32, pp. 2059 - 2071, June 2010. [pdf]
Last updated Oct 16, 2018. |
|||||
|
|
|
|
||||